It Wasn't Me—It Was the Multi-Armed Man: How Intelligent Selection Can Enhance Your Testing

In this industry, we all need to know if our actions produce the results we want, and, frankly, we’d like to know quickly. Gone are the days of slow, trial & error testing. Today, we can systematically test our actions in advance. In marketing, A\B\n and multivariate testing have been used for decades to quantitatively compare the effects of one or more messages against each other and against a control, i.e. no message at all. In digital marketing especially, subject line testing and similar kinds of copy testing have never been easier.

But, there are details to consider. How much data do you need to perform a meaningful test? The rule of thumb has been to send 10% of the audience message A and 10% message B. After measuring the results, you send the “better” message to the remaining 80%. But is 10% even enough? Have you even detected a meaningful difference? Conversely, could 10% for each test group be too much? Have you wasted lots of opportunities with your users by testing a clearly inferior message? Each message and its resulting response or lack thereof constitutes a data point (or datum if you’re fancy) that can be used to learn and improve. So why use ad hoc rules that don’t leverage this valuable signal? With Intelligent Selection by Braze, we can systematically test our actions in advance, rather than just learning slowly through trial and error.

Intelligent Selection treats deciding what message to send users as a Multi-Armed Bandit problem—a famous scenario originally conceived during World War II. Imagine I’m in front of a row of slot machines holding 100 quarters. I can play the machines one at a time in any order. If I win, I get a dollar back. Otherwise, I get nothing. The catch is that all the machines have different odds of winning, and I have no idea what they are at the start. If I put my first quarter into a randomly chosen machine and win, I might put a second quarter into the same machine. But the second time, what if I lose? Should I keep spending more of my quarters at this machine? What if the first win was just a fluke, and some of the other machines have higher payout probabilities? I need to spend more quarters to explore the other options. Or, we can continue exploiting the machines for which we already know something about the payout probability. You can see why this is known as an exploration vs. exploitation problem, and it’s a good analogy for choosing which marketing message might be best.

There’s a solution to this conundrum called Thompson sampling. Developed in the academic domain of Artificial Intelligence, Thompson sampling starts out by assuming all the options are equally as good and sends some test messages in equal proportions across the various options. It then takes a look at the history of payouts of each of the options and calculates their probabilities. Using this information, it creates a Monte Carlo simulation—tens of thousands of virtual drawings from simulated slot machines* with the same statistical properties as the real data observed so far. (The same approach is depicted in an episode of Black Mirror.) The algorithm then looks at the outcomes of those simulations and computes what percent of time we would’ve lost money despite having chosen the apparently “best” option. It then assigns a proportional number of future plays to those options that, though they appear inferior at the moment, might be better than they currently seem due to a lack of information.

The algorithm repeats this process until there’s enough data to conclude that continuing to explore is unnecessary and likely wasteful. At that point, the winner is determined and the test is over. But if we’re not sure, we continue assigning some proportion of plays to the less well understood alternatives. In certain settings, Thompson sampling has been shown to be the best possible approach. It ensures that I reduce the number of messages required to pick a winner. It also allows me to stop or modify my test sooner rather than later if I learn that there is no clear winner.

Importantly, Thompson Sampling makes sure that I adequately test all the alternatives without making a decision too quickly. In a traditional A/B test, it can often be tempting to simply pick the message with a higher conversion rate and call it the winner. For example, if message A yielded a conversion rate of 14% and message B 15%, B must be better, right? Unfortunately, it’s not that easy. It depends on how many users we’ve sampled and how big the real difference, if it exists at all, actually is. This is just another way of saying we don’t necessarily know if the difference we’ve observed is statistically significant. Thompson sampling ensures we incorporate each chunk of new data as it comes in, update our understanding of the effectiveness of each message, and continue doing so until we have a mathematically justifiable winner to choose.

Braze’s solution lets the data tell me how much testing is required rather than using assumptions based on unreliable rules of thumb. With Intelligent Selection, I can be certain that I’m learning as quickly as I can about my alternatives and ensuring that as many users as possible get the right message.

*Extra Detail for the Curious

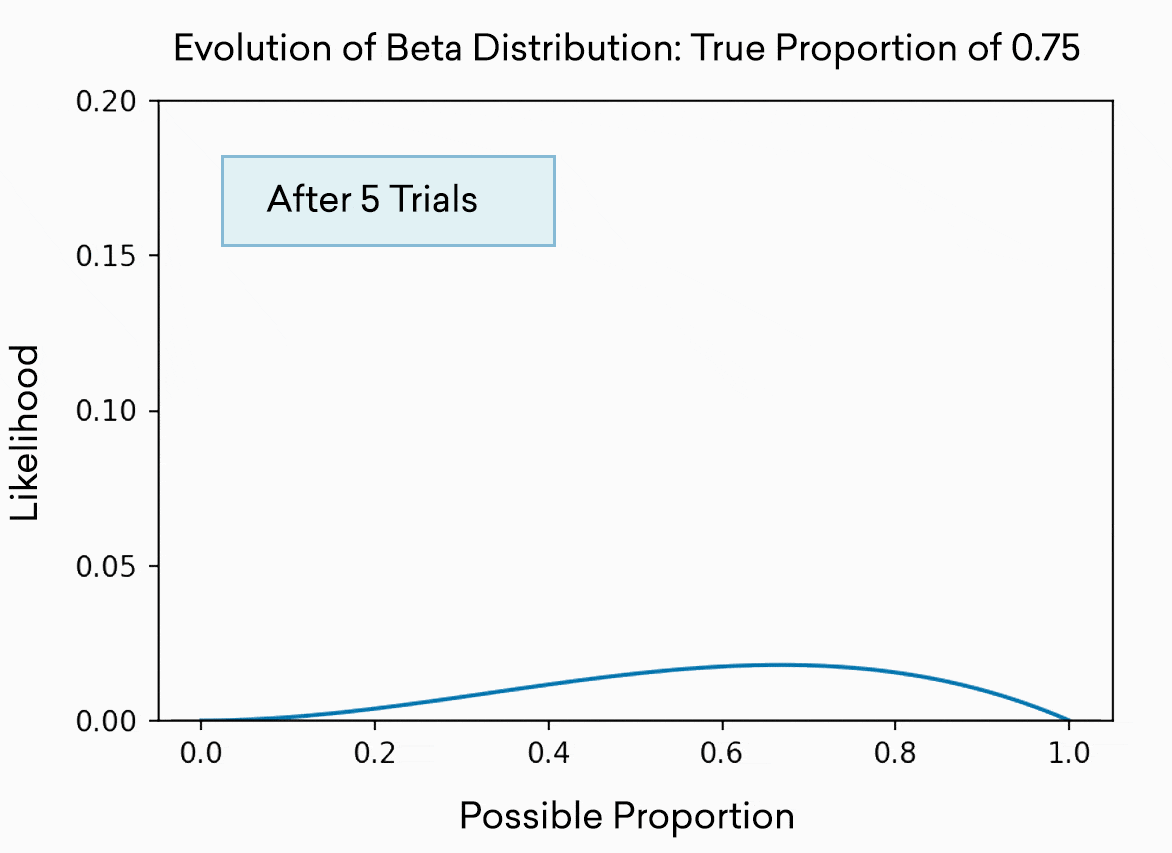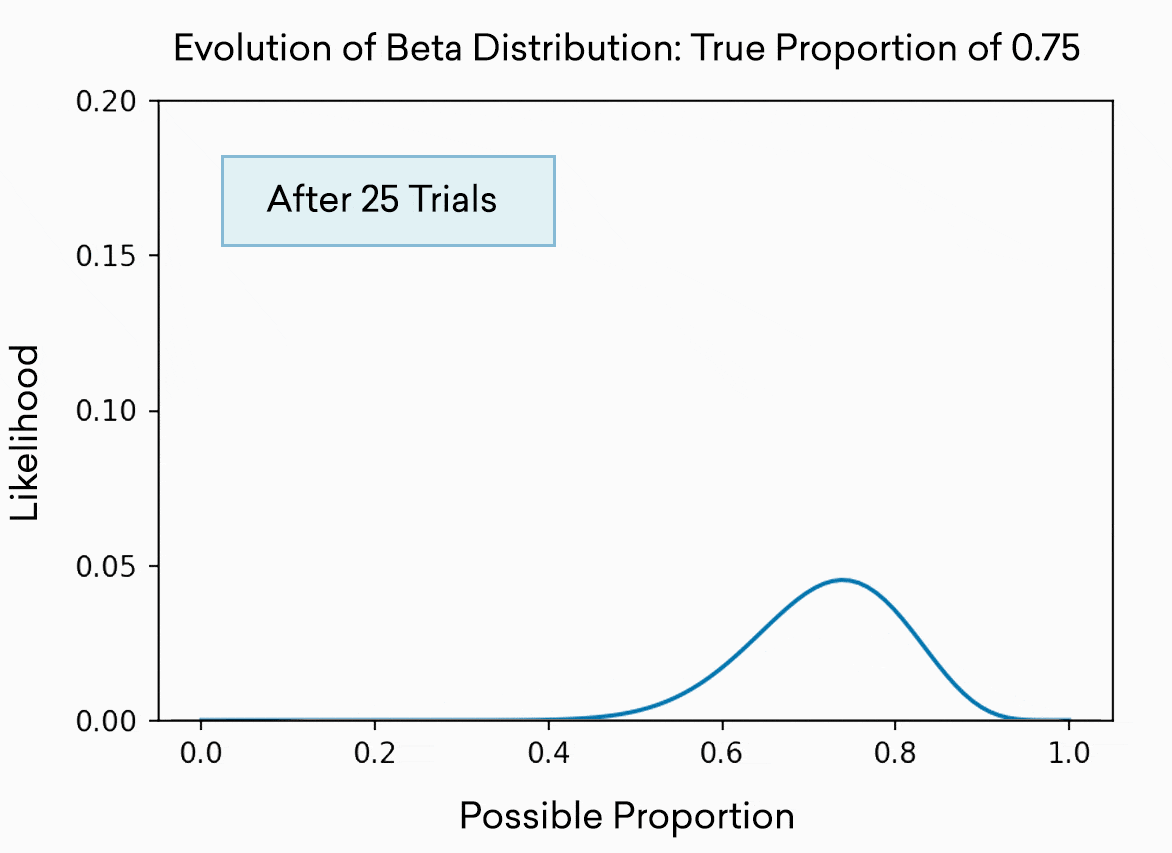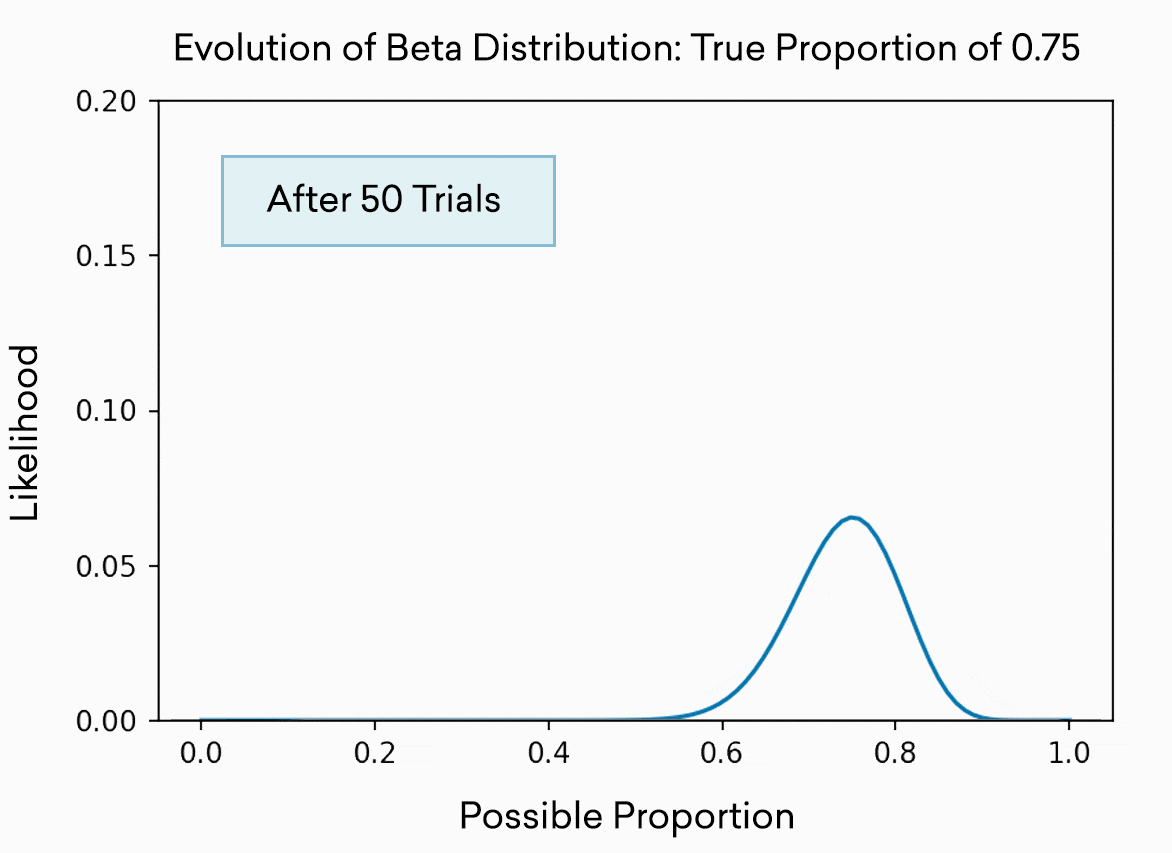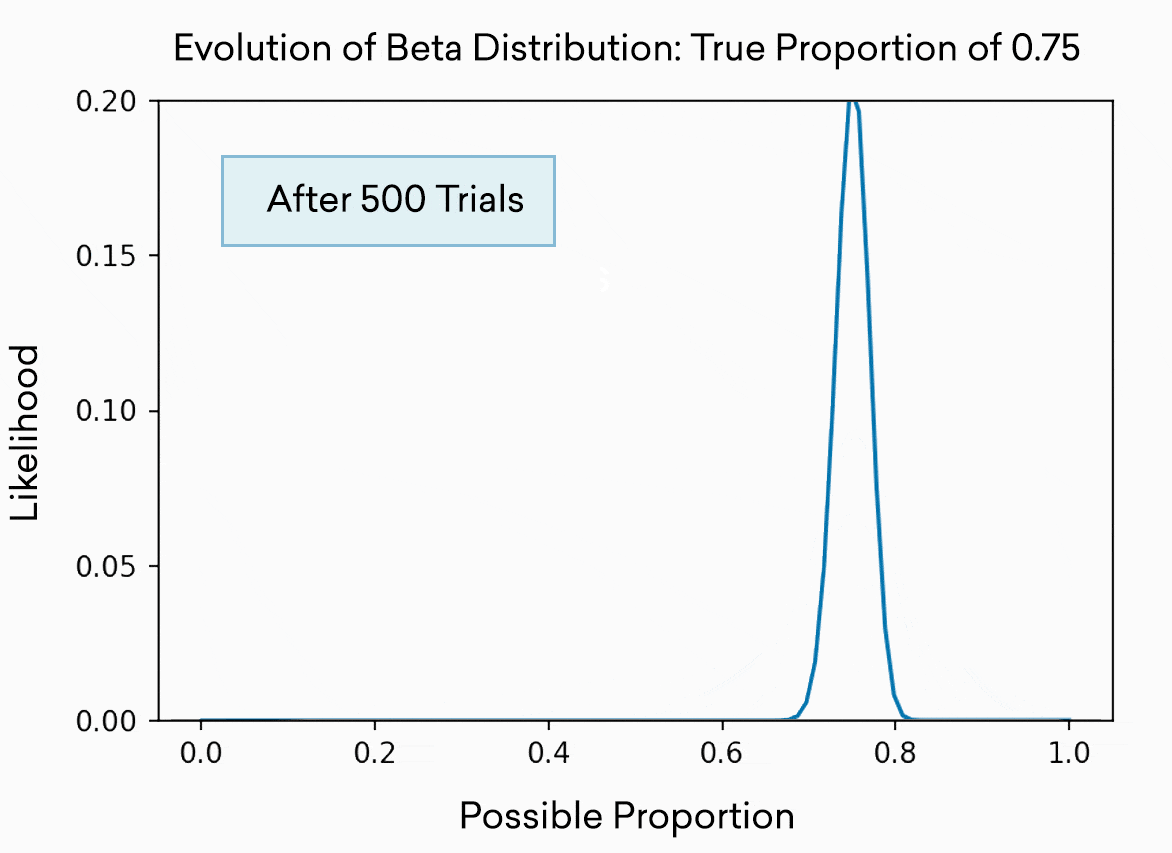
Each slot machine is simulated as a pull from the beta distribution. This distribution is often used to represent the best guess of a proportion or percentage. As you might expect, the more trials you run, the more accurately you know the “true” or “real” percentage, and thus the narrower the distribution becomes. The distribution is effectively the range in which the available evidence indicates the true percentage probably resides. At the beginning, after only 5 trials, it could be almost anywhere between 0 and 1, and our confidence (the height on the y axis) about any one location is low. After 500 trials, we’re pretty sure the true percentage lives somewhere in the range 0.7 to 0.8. Of course, in this toy example, we know the percentage because we set it to 0.75.

Interested in working at Braze? Check out our current job openings!